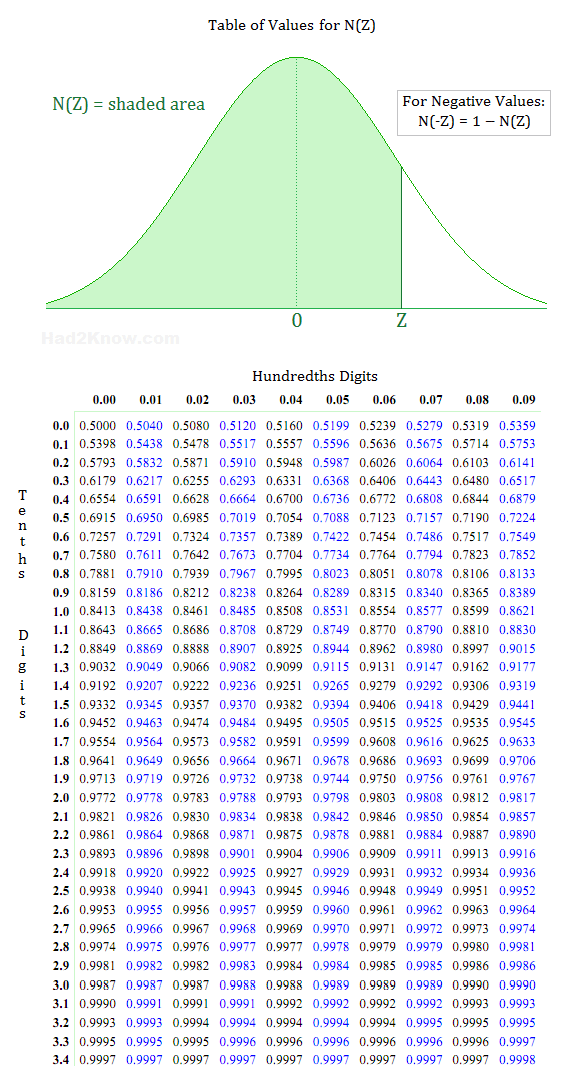
(when x is greater than μ, the corresponding z-score is positive. When z is positive, x is greater than or to the right of μ.Notice that: 5 + (–0.67)(6) is approximately equal to 1. (This has the pattern μ + zσ = raw data.) This means that x = 1 is 0.67 standard deviations (–0.67σ) below or to the left of the mean μ = 5. (given that the standard deviation is σ = 6. This means that x = 17 is two standard deviations (2σ) above or to the right of the mean μ = 5. This says that x is a normally distributed random variable with mean μ = 5 and standard deviation σ = 6.ġ.